स्वागत है त्रिकोणमिति [ trigonometry in Hindi ] त्रिकोणमिति के सभी सूत्र [ trigonometry formulas in Hindi ] में त्रिकोणमिति से संबंधित सभी महत्वपूर्ण जानकारी दी गई है।
त्रिकोणमिति किसे कहते हैं ?
त्रिभुज और इसके कोणों का मापन त्रिकोणमिति कहलाता है अर्थात् त्रिकोणमिति में हम त्रिभुज के गुणधर्मों का अध्ययन करते हैं , जिसमें भुजाओं की लम्बाईयाँ तथा कोण इत्यादि सम्मिलित हैं ।
त्रिकोणमितीय अनुपात [ Trigonometric ratio ] त्रिकोणमितीय अनुपात क्या है?
एक समकोण त्रिभुज के न्यून कोणों के सापेक्ष त्रिभुज की भुजाओं का अनुपात कोणों का त्रिकोणमितीय अनुपात कहलाता है।
किसी समकोण त्रिभुज △ABC में
यदि कोण ∠CAB ,तो
sin θ = B C A C \sin\theta= \frac{BC}{AC} sin θ = A C BC cos θ = A B A C \cos\theta= \frac{AB}{AC} cos θ = A C A B tan θ = B C A B \tan\theta= \frac{BC}{AB} tan θ = A B BC c o s e c θ = A C B C cosec \theta= \frac{AC}{BC} cosec θ = BC A C sec θ = A C A B \sec \theta= \frac{AC}{AB} sec θ = A B A C cot θ = A B B C \cot \theta= \frac{AB}{BC} cot θ = BC A B ( 1 ) त्रिकोणमितीय अनुपातों ( फलन ) के मध्य सम्बन्ध (i) sinθ.cosec θ = 1
(ii) tan θ .cot θ = 1
(iii) cos θ. sec θ = 1
(iv) tan θ = sin θ/cos θ
त्रिकोणमितीय सर्वसमिकाएँ ( Trigonometric Identities ) वह त्रिकोणमितीय सर्वसमिकाएँ जो कोण के सभी मानों के लिए सत्य है ।
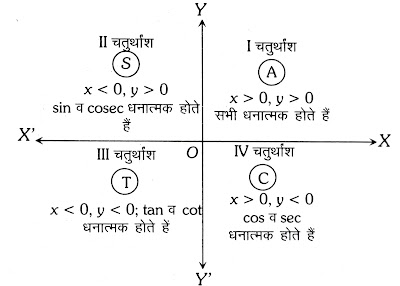
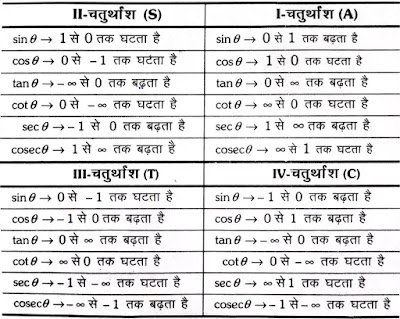
sin 2 θ + cos 2 θ = 1 \sin^2\theta+\cos^2\theta=1 sin 2 θ + cos 2 θ = 1 sec 2 θ − tan 2 θ = 1 \sec^2\theta-\tan^2\theta=1 sec 2 θ − tan 2 θ = 1 c o s e c 2 θ − cot 2 θ = 1 cosec^2\theta-\cot^2\theta=1 cose c 2 θ − cot 2 θ = 1 चतुर्थाशों में त्रिकोणमितीय अनुपातों के चिह-
त्रिकोणमितीय अनुपातों के कोणों के मान θ 0 O 30O 45O 60O 90O sin x 0 1/2 1/√ 2 √3/2 1 cos x 1 √3/2 1/√ 2 1/2 0 tan x 0 1/√3 1 √3 ∞ cot x ∞ √3 1 1/√3 0 cosec x ∞ 2 √ 2 2/√3 1 sec x 1 2/√3 √ 2 2 ∞
त्रिकोणमिति के सभी सूत्र [trigonometry formulas in Hindi ] त्रिकोणमिति फार्मूला, त्रिकोणमिति के सभी फार्मूला जो बहुत महत्वपूर्ण है
दो कोणों के मध्य त्रिकोणमितीय अनुपात त्रिकोणमिति के फार्मूला के प्रकार
योग व अन्तर के सूत्र (Formulae of Sum and Difference) sin ( A + B ) = sin A cos B + cos A sin B \sin (A+B)=\sin A \cos B+\cos A \sin B sin ( A + B ) = sin A cos B + cos A sin B sin ( A − B ) = sin A cos B − cos A sin B \sin (A-B)=\sin A \cos B-\cos A \sin B sin ( A − B ) = sin A cos B − cos A sin B cos ( A + B ) = cos A cos B − sin A sin B \cos (A+B)=\cos A \cos B-\sin A \sin B cos ( A + B ) = cos A cos B − sin A sin B cos ( A − B ) = cos A cos B + sin A sin B \cos (A-B)=\cos A \cos B+\sin A \sin B cos ( A − B ) = cos A cos B + sin A sin B tan ( A + B ) = tan A + tan B 1 − tan A tan B \tan (A+B)=\frac{\tan A+\tan B}{1-\tan A \tan B} tan ( A + B ) = 1 − tan A tan B tan A + tan B tan ( A − B ) = tan A − tan B 1 + tan A tan B \tan (A-B)=\frac{\tan A-\tan B}{1+\tan A \tan B} tan ( A − B ) = 1 + tan A tan B tan A − tan B cot ( A + B ) = cot A cot B − 1 cot A + cot B \cot (A+B)=\frac{\cot A \cot B-1}{\cot A+\cot B} cot ( A + B ) = cot A + cot B cot A cot B − 1 cot ( A − B ) = cot A cot B + 1 cot B − cot A \cot (A-B)=\frac{\cot A \cot B+1}{\cot B-\cot A} cot ( A − B ) = cot B − cot A cot A cot B + 1 tan ( A + B + C ) = tan A + tan B + tan C − tan A tan B tan C 1 − tan A tan B − tan B tan C − tan C tan A \tan (A+B+C)=\frac{\tan A+\tan B+\tan C-\tan A \tan B \tan C}{1-\tan A \tan B-\tan B \tan C-\tan C \tan A} tan ( A + B + C ) = 1 − tan A tan B − tan B tan C − tan C tan A tan A + tan B + tan C − tan A tan B tan C योग व अन्तर का गुणनफल में रूपान्तरण (Transformation of Sum and Difference into Multiplication) sin C + sin D = 2 sin C + D 2 cos C − D 2 \sin C+\sin D=2 \sin \frac{C+D}{2} \cos \frac{C-D}{2} sin C + sin D = 2 sin 2 C + D cos 2 C − D sin C − sin D = 2 cos C + D 2 sin C − D 2 \sin C-\sin D=2 \cos \frac{C+D}{2} \sin \frac{C-D}{2} sin C − sin D = 2 cos 2 C + D sin 2 C − D cos C + cos D = 2 cos C + D 2 cos C − D 2 \cos C+\cos D=2 \cos \frac{C+D}{2} \cos \frac{C-D}{2} cos C + cos D = 2 cos 2 C + D cos 2 C − D cos C − cos D = − 2 sin C + D 2 sin C − D 2 \cos C-\cos D=-2 \sin \frac{C+D}{2} \sin \frac{C-D}{2} cos C − cos D = − 2 sin 2 C + D sin 2 C − D sin ( A + B ) sin ( A − B ) = sin 2 A − sin 2 B = cos 2 B − cos 2 A \sin (A+B) \sin (A-B)
=\sin ^{2} A-\sin ^{2} B
=\cos ^{2} B-\cos ^{2} A sin ( A + B ) sin ( A − B ) = sin 2 A − sin 2 B = cos 2 B − cos 2 A cos ( A + B ) cos ( A − B ) = cos 2 A − sin 2 B = cos 2 B − sin 2 A \cos (A+B) \cos (A-B)
=\cos ^{2} A-\sin ^{2} B
=\cos ^{2} B-\sin ^{2} A cos ( A + B ) cos ( A − B ) = cos 2 A − sin 2 B = cos 2 B − sin 2 A sin ( 6 0 ∘ − A ) sin ( 6 0 ∘ + A ) = sin 3 A 4 sin A \sin \left(60^{\circ}-A\right) \sin \left(60^{\circ}+A\right)=\frac{\sin 3 A}{4 \sin A}
sin ( 6 0 ∘ − A ) sin ( 6 0 ∘ + A ) = 4 sin A sin 3 A cos ( 6 0 ∘ − A ) cos ( 6 0 ∘ + A ) = cos 3 A 4 cos A \cos \left(60^{\circ}-A\right) \cos \left(60^{\circ}+A\right)=\frac{\cos 3 A}{4 \cos A} cos ( 6 0 ∘ − A ) cos ( 6 0 ∘ + A ) = 4 cos A cos 3 A tan ( 6 0 ∘ − A ) tan ( 6 0 ∘ + A ) = tan 3 A tan A \tan \left(60^{\circ}-A\right) \tan \left(60^{\circ}+A\right)=\frac{\tan 3 A}{\tan A} tan ( 6 0 ∘ − A ) tan ( 6 0 ∘ + A ) = tan A tan 3 A गुणनफल का योग और अंतर में रूपांतरण (Transformation of Multiplication into Sum and Difference) 2 sin A cos B = sin ( A + B ) + sin ( A − B ) 2 \sin A \cos B=\sin (A+B)+\sin (A-B) 2 sin A cos B = sin ( A + B ) + sin ( A − B ) 2 cos A sin B = sin ( A + B ) − sin ( A − B ) 2 \cos A \sin B=\sin (A+B)-\sin (A-B) 2 cos A sin B = sin ( A + B ) − sin ( A − B ) 2 cos A cos B = cos ( A + B ) + cos ( A − B ) 2 \cos A \cos B=\cos (A+B)+\cos (A-B) 2 cos A cos B = cos ( A + B ) + cos ( A − B ) 2 sin A sin B = cos ( A − B ) − cos ( A + B ) 2 \sin A \sin B=\cos (A-B)-\cos (A+B) 2 sin A sin B = cos ( A − B ) − cos ( A + B ) कुछ अन्य महत्वपूर्ण सूत्र Some Other Important Formulas sin 2 A = 2 sin A cos A = 2 tan A 1 + tan 2 A \sin 2 A=2 \sin A \cos A=\frac{2 \tan A}{1+\tan ^{2} A} sin 2 A = 2 sin A cos A = 1 + tan 2 A 2 tan A cos 2 A = cos 2 A − sin 2 A = 1 − tan 2 A 1 + tan 2 A = 2 cos 2 A − 1 = 1 − 2 sin 2 A \cos 2 A=\cos ^{2} A-\sin ^{2} A=\frac{1-\tan ^{2} A}{1+\tan ^{2} A}=2 \cos ^{2} A-1=1-2 \sin ^{2} A cos 2 A = cos 2 A − sin 2 A = 1 + tan 2 A 1 − tan 2 A = 2 cos 2 A − 1 = 1 − 2 sin 2 A 1 + sin 2 A = ( sin A + cos A ) 2 1+\sin 2 A=(\sin A+\cos A)^{2} 1 + sin 2 A = ( sin A + cos A ) 2 1 − sin 2 A = ( sin A − cos A ) 2 1-\sin 2 A=(\sin A-\cos A)^{2} 1 − sin 2 A = ( sin A − cos A ) 2 tan 2 A = 2 tan A 1 − tan 2 A \tan 2 A=\frac{2 \tan A}{1-\tan ^{2} A} tan 2 A = 1 − tan 2 A 2 tan A sin 3 A = 3 sin A − 4 sin 3 A \sin 3 A=3 \sin A-4 \sin ^{3} A sin 3 A = 3 sin A − 4 sin 3 A cos 3 A = 4 cos 3 A − 3 cos A \cos 3 A=4 \cos ^{3} A-3 \cos A cos 3 A = 4 cos 3 A − 3 cos A tan 3 A = 3 tan A − tan 8 A 1 − 8 tan 2 A \tan 3 A=\frac{3 \tan A-\tan ^{8} A}{1-8 \tan ^{2} A} tan 3 A = 1 − 8 tan 2 A 3 tan A − tan 8 A
आपका , इस पोस्ट त्रिकोणमिति [ trigonometry in Hindi ] त्रिकोणमिति के सभी सूत्र [ trigonometry formulas in Hindi ] में त्रिकोणमिति से संबंधित सभी महत्वपूर्ण जानकारी दी गई है। ![त्रिकोणमिति [ trigonometry in Hindi ] त्रिकोणमिति के सभी सूत्र](https://1.bp.blogspot.com/-X_1Qk06p9Tw/YJ_3NnPEYbI/AAAAAAAABRQ/YwMfVq07ECc_Llln8XJWsvBj4Dfy60vLQCLcBGAsYHQ/w320-h320/%25E0%25A4%25A4%25E0%25A5%258D%25E0%25A4%25B0%25E0%25A4%25BF%25E0%25A4%2595%25E0%25A5%258B%25E0%25A4%25A3%25E0%25A4%25AE%25E0%25A4%25BF%25E0%25A4%25A4%25E0%25A4%25BF%2B%25E0%25A4%2595%25E0%25A5%2587%2B%25E0%25A4%25B8%25E0%25A4%25AD%25E0%25A5%2580%2B%25E0%25A4%25B8%25E0%25A5%2582%25E0%25A4%25A4%25E0%25A5%258D%25E0%25A4%25B0.webp "त्रिकोणमिति [ trigonometry in Hindi ] त्रिकोणमिति के सभी सूत्र")
I am very happy.
Ap ne bahut acchi PDF banayi hai