सरल लोलक [ Simple Pendulum in Hindi ] सरल लोलक का आवर्तकाल

सरल लोलक (Simple Pendulum in Hindi ) सरल लोलक का आवर्तकाल यहाँ सरल लोलक (Simple Pendulum in Hindi ) सरल लोलक का आवर्तकाल से संबंधित सभी महत्वपूर्ण जानकारी दी गई है। 

इस आर्टिकल में सरल लोलक (Simple Pendulum in Hindi ) सरल लोलक का आवर्तकाल से सम्बंधित परिभाषाये ,एक सरल आवर्त गति करने वाले सरल लोलक का आवर्तकाल व आवृति सरल लोलक का आवर्तकाल का व्यंजक ज्ञात कीजिए को समावेश किया है

सरल लोलक (Simple Pendulum) 

सरल लोलक किसे कहते हैं ?

यदि किसी पदार्थ के भारी (लेकिन बिन्दु समान) कण को एक भारहीन, लम्बाई में न बढने वाली अतन्य डोरी के एक सिरे से बाँधकर किसी दूढ़ आधार से लटका दें, तो उसे सरल लोलक कहते हैं।

माना m द्रव्यमान के एक गोलक ( बिन्दु द्रव्यमान ) को । लम्बाई की डोरी लटकाया गया है । माध्य स्थिति से θ कोणीय विस्थापन की स्थिति में गोलक का रेखीय विस्थापन x है ।

सरल लोलक का चित्र-

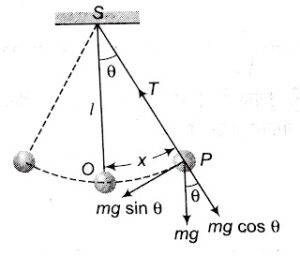
एक सरल आवर्त गति करने वाले सरल लोलक का आवर्तकाल व आवृति

सरल लोलक का आवर्तकाल का सूत्र

T=2 \pi \sqrt{\frac{l}{g}}

और

v=\frac{1}{2 \pi} \sqrt{\frac{g}{l}}

सरल लोलक का आवर्तकाल का व्यंजक ज्ञात कीजिए

चित्र से –

गोलक पर कार्यरत प्रत्यानयन बल

F = -mg \sin\theta

कोण अत्यंत सूक्ष्म हो तब

\sin\theta=\theta=\frac{x}{l}

\therefore

F=-m g \cdot \frac{x}{l}

\frac{F}{m}=A=-\frac{g}{l} x.....(1)

सरल आवर्त गति करते कण का त्वरण

A=-\frac{k}{m} \cdot x.......(2)

समी (i) व (ii) से

\frac{k}{m}=\frac{g}{l}

\omega=\sqrt{\frac{k}{m}}=\sqrt{\frac{g}{l}}

अत: आवर्तकाल 

(T)=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{m}{k}}

T=2 \pi \sqrt{\frac{l}{g}}

ऊर्जा विधि (Energy Method) 

माना θ विस्थापन पर कण का कोणीय वेग है। स्थिति A पर कण कुल यांत्रिक ऊर्जा

E=\frac{1}{2} I \omega^{2}+m g\left(h_{A}-h_{C}\right)

या

E=\frac{1}{2}\left(m l^{2}\right) \omega^{2}+m g l(1-\cos \theta)

E\space\space नियत \space है, \spaceअत: \frac{d E}{d t}=0

या

0=m l^{2} \omega\left(\frac{d \omega}{d t}\right)+m g l \sin \theta\left(\frac{d \theta}{d t}\right)

\frac{d \theta}{d t}=\omega, \frac{d \omega}{d t}=\alpha \space \spaceतथा  \space \space\sin \theta \approx \theta

उपरोक्त व्यंजक में रखने पर

\alpha=-\left(\frac{g}{l}\right) \theta

T=2 \pi \sqrt{\frac{\theta}{\alpha}}

T=2 \pi \sqrt{\frac{l}{g}}

सरल लोलक के आवर्तकाल को प्रभावित करने वाले कारक

👉यदि l लम्बाई के लोलक का θ^∘C पर आवर्तकाल T हो तथा तापमान △θ^∘C बढ़ने पर आवर्तकाल T+△T हो, तो

\frac{\Delta T}{T}=\frac{1}{2} \alpha \cdot \Delta \theta

यहाँ, alpha रेखीय प्रसार गुणांक है। 

सेकण्ड लोलक आवर्तकाल 2 सेकण्ड होता है। जहाँ g=9.8 मी/से² हो, वहाँ सेकण्ड लोलक की लम्बाई 0.9929 मी (लगभग 1 मी) होती है। 

👉यदि किसी सरल लोलक के गोलक का घनत्व ρ है तथा यह σ(σ<p) घनत्व वाले द्रव में दोलन करता है, तो वायु में आवर्तकाल की तुलना में द्रव में आवर्तकाल बढ़ जायेगा। द्रव में आवर्तकाल

T=2 \pi \sqrt{\frac{l}{g\left(1-\frac{\sigma}{\rho}\right)}}

👉यदि लिफ्ट की छत से कोई लोलक लटका है एवं लिफ्ट का ऊध्वाधर त्वरण a है, तो आवर्तकाल

T=2 \pi \sqrt{\frac{1}{(g \pm a)}}

यहाँ धनात्मक चिन्ह ऊपर की ओर त्वरण के लिये तथा ऋणात्मक चिन्ह नीचे की ओर त्वरण के लिये प्रयोग किया जाता है। 

👉यदि लिफ्ट मुक्त रूप से गिर रही हो, तो लोलक का आवर्तकाल अनन्त होता है। यदि लोलक के दोलक का द्रव्यमान m व आवेश q है तथा वह ऊर्ध्वाधर विद्युत क्षेत्र E में दोलन करता है, तो आवर्तकाल

T=2 \pi \sqrt{\frac{l}{\left(g \pm \frac{q E}{m}\right)}}

यहाँ धनात्मक चिन्ह = यदि E की दिशा ऊर्ध्वाधर नीचे की ओर है तथा ऋणात्मक चिन्ह = यदि E की दिशा ऊर्ध्वाधर ऊपर की ओर है। 

👉यदि उपरोक्त लोलक क्षैतिज विद्युत क्षेत्र में दोलन करता है, तो आवर्तकाल 

T=2 \pi \sqrt{\frac{l}{g^{2}+\frac{q^{2} E^{2}}{m^{2}}}}

👉बहुत अधिक लम्बाई l→∞ के सरल लोलक का आवर्तकाल

T=2 \pi \sqrt{\frac{R}{g}}=84.6   मिनट 

यहाँ, R= पृथ्वी की त्रिज्या