वृत्तीय गति किसे कहते हैं ? ( Circular Motion in Hindi )

वृत्तीय गति  किसे कहते हैं ? ( Circular Motion in Hindi ) स्वागत है 🙏आपका , इस पोस्ट में वृत्तीय गति ( Circular Motion ) से संबंधित सभी महत्वपूर्ण जानकारी दी गई है। 

वृत्तीय गति ( Circular Motion ) किसे कहते हैं ? 

जब कोई कण वृत्त की परिधि के अनुदिश गति करता है, तो इस गति को वृत्तीय गति कहते हैं। वृत्तीय गति, द्विविमीय गति अथवा एक तल में गति है। 

इस आर्टिकल में  वृत्तीय गति ( Circular Motion ) से सम्बंधित परिभाषाये , वृत्तीय गति ( Circular Motion )के कुछ महत्वपूर्ण बिंदु ,  वृत्तीय गति ( Circular Motion ) के कुछ महत्वपूर्ण सूत्र को समावेश किया है, साथ में सभी महत्वपूर्ण सूत्र को अच्छे से लिखा गया है। फिर यदि कोई गलती है तो नीचे कमेंट में जरूर बताये ।

वृत्तीय गति ( Circular Motion )किसे कहते हैं ?

वृत्तीय गति की परिभाषा (Definition of Circular Motion) 

जब कोई कण वृत्त की परिधि के अनुदिश गति करता है, तो इस गति को वृत्तीय गति कहते हैं। 

वृत्तीय गति, द्विविमीय गति अथवा एक तल में गति है। 

इस गति में वेग की दिश लगातार परिवर्तित होती रहती है।

वृत्तीय गति से संबंधित कुछ महत्वपूर्ण परिभाषाएं

कोणीय चर (Angular Variables)

(i) कोणीय विस्थापन (Angular displacement) 

कण की प्रारम्भिक व अन्तिम स्थितियो के मध्य का कोण, जो कण द्वारा घ्रूर्णन अक्ष पर अन्तरित होता है, उसे कोणीय विस्थापन कहते हैं।

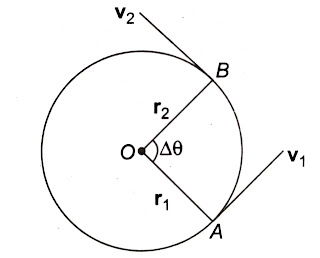
 चित्रानुसार स्थिति सदिश OA व OB के मध्य कोणीय विस्थापन \Delta \theta है। इसे सामान्यतया: रेडियन में मापा जाता है।

(ii) कोणीय वेग (Angular velocity) 

कोणीय विस्थापन के परिवर्तन की दर कोणीय वेग कहलाती है। अत: कोणीय वेग 

\omega=\lim_{\triangle t \rightarrow 0}\frac{\triangle\theta}{\triangle t}=\frac{d\theta}{dt}

यह एक अक्षीय सदिश है जिसकी दिशा दक्षिण हस्त नियम से ज्ञात की जाती है। 

इसकी इकाई रेडियन/से है।

(iii) कोणीय त्वरण (Angular acceleration) 

कोणीय वेग परिवर्तन की दर कोणीय त्वरण कहलाती है। अत: कोणीय त्वरण

\alpha=\frac{d\omega}{dt}=\frac{d^2\theta}{dt^2}

इसकी इकाई रेडियन/से² है।

यदि कोणीय त्वरण alpha नियत हो, तो

\theta=\omega_{0} t+\frac{1}{2} \alpha t^{2}

\omega=\omega_{0}+\alpha t

तथा

\omega^{2}=\omega_{0}^{2}+2 \alpha \theta

जहाँ ω₀ तथा ω क्रमश: t=0 तथा समय t पर कोणीय वेग हैं तथ θ समय t का कोणीय विस्थापन है।

वृत्तीय गति से संबंधित पद (Terms Related to Circular Motion)

वेग (Velocity)

वृत्तीय गति में दो प्रकार के वेग होते हैं-रेखीय वेग तथ कोणीय वेग।

(i) रेखीय वेग (v) तथा रेखीय चाल (v)

\mathbf{v}=\frac{d \mathbf{s}}{d t}

तथा 

 \quad v=|\mathbf{v}|=\left|\frac{d \mathbf{s}}{d t}\right|

(ii) कोणीय वेग ω₀ तथा कोणीय चाल ( ω)

\omega=|\omega|=\left|\frac{\mathbf{d} \theta}{d t}\right|

=\frac{d \theta}{d t}

रेखीय चाल (v) तथा कोणीय चाल ω में सम्बन्ध

जहाँ r= कण का वृत्त के केन्द्र के सापेक्ष स्थिति सदिश

त्वरण  (Acceleration)

वृत्तीय गति में त्वरण के दो घटक होते हैं।

(i) स्पशरिखीय त्वरण (Tangential acceleration) (a_t) यह त्वरण का वह घटक है जो कण के वेग के अनुदिश होता है। a_t त्वरण a का वेग v की दिशा में घटक

=\frac{d v}{d t} 

=\frac{d|\mathbf{v}|}{d t}

(ii) त्रिज्यीय त्वरण (Radial acceleration) a_r यह त्वरण का वह घटक है जो वृत्त के केन्द्र की ओर होता है। इसी त्वरण के कारण कण की दिशा बदलती है।

a_{r}=\frac{v^{2}}{r}=r \omega^{2}

वृत्तीय गति के प्रकार (Types of Circular Motion)

वृत्तीय गति तीन प्रकार की हो सकती है।

(i) एकसमान वृत्तीय गति (Uniform circular motion) 

इस प्रकार की गति में कण की चाल नियत रहती है। इसलिए a_t=0 व a_{c}=\frac{v^{2}}{r} या r \omega^{2} होता है। अत: कुल त्वरण a_r के समान ही होता है। a व v के मध्य कोण 90^o होता है।

(ii) वृत्तीय गति जिसमें चाल के मान में वृद्धि हो (Circular motion of increasing speed) 

इस प्रकार की वृत्तीय गति में कण की चाल में वृद्धि होती है अत: a_t का मान धनात्मक या वेग की दिशा में होता है। इस स्थिति में कुल त्वरण

a=\sqrt{a_{t}^{2}+a_{r}^{2}}

जहाँ,

a_{t}=\frac{d v}{d t} \text { और } \frac{d|\mathbf{v}|}{d t}

(iii) वृत्तीय गति जिसमें चाल के मान में कमी हो (Circular motion of decreasing speed) 

इस प्रकार की वृत्तीय गति में कण की चाल में कमी होती जाती है।। अत: a_t का मान ऋणात्मक या वेग की दिशा के विपरीत होता है। इस स्थिति में कुल त्वरण

a=\sqrt{a_{t}^{2}+a_{r}^{2}}