जड़त्व आघूर्ण ( Moment of Inertia in Hindi ) जड़त्व आघूर्ण किसे कहते हैं ?

जड़त्व आघूर्ण ( Moment of Inertia in Hindi  ) जड़त्व आघूर्ण किसे कहते हैं ? इस पोस्ट में जड़त्व आघूर्ण ( Moment of Inertia in Hindi  ) जड़त्व आघूर्ण किसे कहते हैं ?  से संबंधित सभी महत्वपूर्ण जानकारी दी गई है। 

इस आर्टिकल में जड़त्व आघूर्ण ( Moment of Inertia in Hindi  ) जड़त्व आघूर्ण किसे कहते हैं ? से सम्बंधित परिभाषाये ,जड़त्व आघूर्ण ( Moment of Inertia ) के कुछ महत्वपूर्ण बिंदु , जड़त्व आघूर्ण  के कुछ महत्वपूर्ण सूत्र 

जड़त्व आघूर्ण का SI मात्रक क्या है ? जड़त्व आघूर्ण कैसी राशि है ? जड़त्व आघूर्ण सम्बन्धी प्रमेय Theorems Related to Moment of Inertia 1. समान्तर अक्षों का प्रमेय ( Theorem of Parallel Axes ) लम्बवत् अक्षों का प्रमेय ( Theorem of Perpendicular Axes ) ​को समावेश किया है, साथ में सभी महत्वपूर्ण सूत्र को अच्छे से लिखा गया है। फिर भी यदि कोई गलती है तो नीचे कमेंट करके   जरूर बताये ।

जड़त्व आघूर्ण ( Moment of Inertia ) 

घूर्णन गति में वस्तु का वह गुण जिसके कारण वह किसी अक्ष के सापेक्ष अपनी घूर्णन अवस्था में परिवर्तन का विरोध करती है , उस अक्ष के सापेक्ष वस्तु का जड़त्व आघूर्ण कहलाता है । 

👉घूर्णन गति कर रही किसी वस्तु अथवा कण का किसी अक्ष के सापेक्ष जड़त्व आघूर्ण उस वस्तु अथवा कण के द्रव्यमान व घूर्णन अक्ष से दूरी के वर्ग के गुणनफल के बराबर होता है । इसे I से प्रदर्शित करते हैं ।

यदि किसी कण का द्रव्यमान m तथा घूर्णन अक्ष से उसकी दूरी r हो ( चित्र A) , तब कण का घूर्णन अक्ष के सापेक्ष जड़त्व आघूर्ण 

I = m{r}^2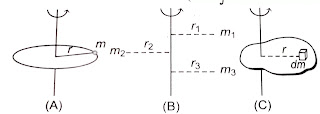

यदि कोई वस्तु अनेक कणों से मिलकर बनी है , जिनके द्रव्यमान क्रमशः m₁ , m₂ , m₃ …. तथा घूर्णन अक्ष से दूरियाँ क्रमश : r₁,r₂,r₃ ….. ( चित्र  B ) हों तब उस वस्तु का घूर्णन अक्ष के परित : जड़त्व आघूर्ण 

I = m_1 {r_1}^2 + m_2 {r_2}^2 + m_3 {r_3}^2 =\sum_{i=1}^{n}m_i {r_2}^2

यदि किसी वस्तु का द्रव्यमान वितरण सतत् ( continuous ) हो ( चित्र C ) , तो घूर्णन अक्ष से । दूरी पर स्थित वस्तु के सूक्ष्म भाग dm को एक कण मानने पर उसका जड़त्व आघूर्ण , dI = dmr² अर्थात् I=∫r²dm

जड़त्व आघूर्ण का SI मात्रक क्या है ?

👉जड़त्व आघूर्ण का मात्रक क्रिया – मी² है । 

I का मान घूर्णन अक्ष के सापेक्ष कणों के द्रव्यमान , कणों की दूरी व घूर्णन अक्ष की स्थिति पर ( वस्तु के द्रव्यमान वितरण पर ) निर्भर करता है । यहाँ द्रव्यमान वितरण का तात्पर्य उसके आकार , आकृति व घनत्व से है । 

👉किसी वस्तु का जड़त्व आघूर्ण जितना अधिक होता है उसकी घूर्णन अवस्था में परिवर्तन हेतु उतना ही अधिक बल आघूर्ण आरोपित करना पड़ेगा ।

जड़त्व आघूर्ण कैसी राशि है ?

👉यह एक सदिश राशि नहीं है क्योंकि दक्षिणावर्ती या वामावर्ती घूर्णन के लिए इसका मान समान होता है परन्तु इसे अदिश भी नहीं कह सकते क्योंकि घूर्णन अक्ष की भिन्न – भिन्न दिशाओं में इसका मान भिन्न – भिन्न होता है । वास्तव में , यह एक प्रदिश ( Tensor ) राशि है ।

जड़त्व आघूर्ण सम्बन्धी प्रमेय ( Theorems Related to Moment of Inertia ) 

1. समान्तर अक्षों का प्रमेय ( Theorem of Parallel Axes ) 

किसी पिण्ड का किसी दिये गये अक्ष के परितः जड़त्व आघूर्ण I उस पिण्ड के द्रव्यमान केन्द्र से गुजरने वाले तथा दिये गये अक्ष के समान्तर किसी अक्ष के परित : जड़त्व आघूर्ण I व पिण्ड के द्रव्यमान M व दोनों अक्षों के मध्य लम्बवत् दूरी a के वर्ग के गुणनफल के योग के तुल्य होता है ।

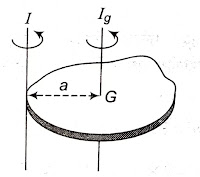
 I = I_g + Ma^2

लम्बवत् अक्षों का प्रमेय ( Theorem of Perpendicular Axes ) 

इस प्रमेय के अनुसार किसी समतल पटल का उसके तल के लम्बवत् किसी अक्ष के परित : जड़त्व आघूर्ण , उसके तल में स्थित दो परस्पर लम्बवत् अक्षों ( जिनके कटान बिन्दु से प्रथम अक्ष गुजरता है ) के परितः जड़त्व आघूर्णां के योग के तुल्य होता है ।

I_z = I_x + I_y 

👉 द्विविमीय सममित वस्तुओं के लिए वस्तु के तल में स्थित व द्रव्यमान केन्द्र से गुजरने वाले सभी अक्षों के परितः जड़त्व आघूर्ण समान होता है । अतः अक्षों का लम्बवत् होना आवश्यक नहीं है । 

👉लम्बवत् अक्ष प्रमेय में तीनों अक्षों ( x , y व z ) का प्रतिच्छेद बिन्दु पिण्ड की सतह पर कोई भी बिन्दु हो सकता है ( यह पिण्ड के बाहर भी स्थित हो सकता है ) यह पिण्ड का द्रव्यमान केन्द्र भी हो सकता है और नहीं भी ।