सरल रेखा में गति [ saral rekha mein gati ] एकविमीय गति

सरल रेखा में गति ( Motion in Straight Line )-एकविमीय गति saral rekha mein gati ek-vimeey gati 

स्वागत है 🙏आपका , इस पोस्ट में सरल रेखा में गति ( Motion in Straight Line )-एकविमीय गति saral rekha mein gati ek-vimeey gati से संबंधित सभी महत्वपूर्ण जानकारी दी गई है। 

सरल रेखीय गति किसे कहते हैं ? एक उदाहरण दीजिए

किसी वस्तु की एक सीधी रेखा में गति को रैखिक गति या सरल रेखा में गति या एकविमीय गति कहा जाता है।

जैसे- सीधी सड़क पर बस की गति।

इस आर्टिकल में सरल रेखीय गति से सम्बंधित परिभाषाये , सरल रेखीय गति के कुछ महत्वपूर्ण बिंदु ,  सरल रेखीय गति के कुछ महत्वपूर्ण सूत्र

सरल रेखीय गति से सम्बंधित परिभाषाये को समावेश किया है, साथ में सभी महत्वपूर्ण सूत्र को अच्छे से लिखा गया है। फिर यदि कोई गलती है तो नीचे कमेंट में जरूर बताये । 

सरल रेखीय गति किसे कहते हैं  ? एकविमीय गति saral rekha mein gati ek-vimeey gati

सरल रेखा में गति ( Motion in Straight Line ) 

सरल रेखा में कण की गति एकविमीय तथा सबसे सरल गति है । इस प्रकार की गति में एक बिन्दुवत वस्तु प्रत्येक क्षण पर एक निश्चित स्थिति प्राप्त करती है । 

अत : कण की गति को किसी स्वेच्छ मूल बिन्दु के सापेक्ष स्थिति ( x ) को संगत समय (t) के फलन के रूप में व्यक्त कर सकते हैं । 

गणितीय रूप में               x = f ( t )

किसी निर्देश तन्त्र में किसी कण की मूलबिन्दु से दूरी ( x ) उसकी स्थिति को प्रदर्शित करती है । मूलबिन्दु की स्थिति के अनुसार उसकी स्थिति धनात्मक या ऋणात्मक भी हो सकती है ।

एकसमान त्वरित गति से चलते पिण्ड के लिए गति के समीकरण 

(Uniformly Accelerated Motion)

v=u+at जहाँ, u= प्रारम्भिक वेग

s=u t+\frac{1}{2} a t^{2}

v=t समय पश्चात् वेग

v^{2}=u^{2}+2 a s

s=t सेकण्ड में चली दूरी s_{t}=u+\frac{1}{2} a(2 t-1) a=त्वरण

s_t=t वें सेकण्ड में चली दूरी मन्दन की अवस्था में a के स्थान पर (-a) लिया जाता है।

सदिश रूप में 

\quad \overrightarrow{\mathbf{v}}=\overrightarrow{\mathbf{u}}+\overrightarrow{\mathbf{a}} t

\overrightarrow{\mathrm{s}}=\overrightarrow{\mathbf{u}} t+\frac{1}{2}\overrightarrow{\mathbf{a}} t^{2}

\vec{v} \cdot \vec{v}=\vec{u} \cdot \vec{u}+2 \vec{a} \cdot \vec{s}

एकसमान त्वरित गति का प्राफीय प्रदर्शन 

(Graphical Representation of Uniformly Accelerated Motion)

वेग- समय ग्राफ (Velocity-Time Graph) 

यदि कोई वस्तु नियत त्वरण के अन्तर्गत गति करे तो इसका वेग-समय ग्राफ एक झुकी रेखा के रूप में होता है। यदि वस्तु का प्रारम्भिक वेग u हो तथा t समय पश्चात् यह v हो जाये, तब

(i) रेखा का ढाल त्वरण के बराबर होता है अर्थात्

m = \tan\theta=\frac{v-u}{t-0}=a

(ii) v-t ग्राफ तथा t-अक्ष के बीच घिरा क्षेत्रफल विस्थापन के बराबर होता है क्योंकि

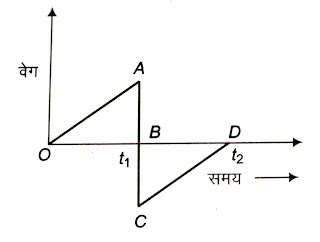
\Delta s=v \Delta t=(O B \times C D)

=(A C \times C D)

= पट्टी ABC का क्षेत्रफल समय t₁ से t₂ तक कुल विस्थापन दिये गये समयान्तराल h₄ व t₂ के बीच सभी पट्टियों के क्षेत्रफलों का योग

= वेग-समय ग्राफ तथा समय-अक्ष के बीच घिरा क्षेत्रफल

👉यदि वस्तु ऊर्ध्वाधर नीचे की ओर कुछ प्रारम्भिक वेग से फेंकी जाये  तो गति के समीकरण

v=u+g t 

h=u t+\frac{1}{2} g t^{2}

v^{2}=u^{2}+2 g h 

h_{n}=u+\frac{g}{2}(2 n-1)

☝ यदि वस्तु ऊर्वाधर ऊपर की ओर कुछ प्रारम्भिक वेग से फेंकी जाए ती गति के समीकरण g के स्थान पर (- g) का प्रयोग किया जाता है। 

👉यदि पिण्ड को किसी ऊँचाई से स्वतन्रतापूर्वंक छोड़ा जाए तब

v =g t 

h =\frac{1}{2} g t^{2}

v^{2} =2 g h 

h_{n} =\frac{1}{2} g(2 n-1)

उदाहरण . एक ट्रेन की चाल 600 मी दूरी में 12 किमी/घण्टा से 60 किमी/घण्टा बढ़ाने में कितना समय लगेगा जबकि उसका त्वरण नियत है, त्वरण का मान क्या है? 

हल. 

प्रारम्भिक वेग, u=12 \times \frac{5}{18}=\frac{10}{3} मी/से 

अन्तिम वेग, v=60 \times \frac{5}{18}=\frac{50}{3} मी/से

दूरी, s=600 मी 

गति के समीकरण, v²=u²+2as से

\left(\frac{50}{3}\right)^{2}=\left(\frac{10}{3}\right)^{2}+2 a \times 600

\frac{2500}{9}-\frac{100}{9} =1200a 

\frac{2400}{9}=1200 a \Rightarrow a=\frac{2}{9} \text { m/sec }^{2}

समीकरण v=u+at से,

\frac{50}{3}=\frac{10}{3}+\frac{2}{9} \times t

\frac{40}{3}=\frac{2}{9} \times t \Rightarrow t=60  सेकण्ड 

यदि गति में त्वरण परिवर्तनशील हो तब त्वरण

(Non-uniform or Variable Accelerated Motion)

a=\frac{d u}{d t}=\frac{d^{2} x}{d t^{2}}=\frac{v d v}{d x}

यदि त्वरण, समय का फलन हो तो

\int a d t=\int d v

तथा \quad \int dx=\int v dt

यदि त्वरण, वेग का फलन है तो

a=\frac{d v}{d t} 

\int d t=\int \frac{d v}{a}

यदि त्वरण, विस्थापन का फलन है तो

a =v \cdot \frac{d v}{d x} 

\int v d v =\int a d x

ध्यान दें! गति में त्वरण यदि परिवर्ती है तब गति के समीकरगों का प्रयोग नहीं किया जाता है।

सरल रेखा में गति-एक विमीय गति के कुछ महत्वपूर्ण बिंदु 

👉 विस्थापन – समय आरेख का ढाल वेग को प्रदर्शित करता है  V = dx/dt

👉वेग – समय आरेख का ढाल त्वरण को प्रदर्शित करता है a = dv/dt  

👉वेग – समय आरेख व समय अक्ष के मध्य क्षेत्रफल विस्थापन को प्रदर्शित करता है ।  

👉त्वरण – समय आरेख व समय अक्ष के मध्य क्षेत्रफल वेग में परिवर्तन को प्रदर्शित करता है । 

👉एकसमान गति के लिये विस्थापन – समय आरेख सरल रेखा होता है । ये मूल बिन्दु से गुजरता है यदि t = 0 पर विस्थापन शून्य हो ।

👉एकसमान त्वरित गति में वेग – समय आरेख एक सरल रेखा होती है । ये रेखा मूल बिन्दु से गुजरती है , यदि t = 0 पर प्रारम्भिक वेग u का मान शून्य होता है । यदि प्रारम्भिक वेग शून्य नहीं हो तो रेखा मूलबिन्दु से पारित नहीं होती है ।

👉एकसमान त्वरित या मंदित गति में विस्थापन – समय का आरेख एक परवलय होता है

( चूँकि s = ut +1/2at² )